近接勾配法応用編その3～トレースノルム正則化項付きロジスティック回帰による行列データの分類～

はじめに

前回の記事では、ベクトルデータの分類問題に対するスパースなロジスティック回帰を説明しましたが、今回はその拡張となる行列データに対するロジスティック回帰を見ていきます。この行列データ分類問題においても正則化項は重要な役割を持ちますが、中でもトレースノルムの正則化項を用いることで低ランクな解が得られ、多次元の時系列データの分類などに有効であることを見ていきます。

行列データの分類

まず、学習データ集合 $\left\{{\bf X}_i, y_i \right\}$ $(i=1⋯N)$ があるとします。ここで、 ${\bf X}$ は $D \times T$ の行列、 $y$ は $y \in \left\{0,1 \right\}$ のラベルです。この学習データ集合から係数行列 ${\bf W}$ とバイアス項 $b$ を学習し、以下に示すような線形モデルで分類することが今回のテーマです。

$\displaystyle a({\bf X}) = {\rm Tr}({\bf X}^T {\bf W}) + b \tag{1}$

行列データ分類問題の特徴

では、行列データを直接扱うことにどのようなメリットがあるのでしょうか。確かに、行列データ ${\bf X}$ をベクトルに変換して（列ベクトルを縦に連結するなどして）、学習・分類するという方法も考えられます。しかしベクトルにしてしまうと行列構造がなくなり、行と列の意味合いが異なる場合に重要な情報が失われる可能性があります。
例えば、複数のセンサーから取得される多次元の時系列データの場合、行がセンサー、列が時間に対応する行列データとしてとらえることができます。このようなデータを連結してベクトルとして扱ってしまうと、空間方向と時間方向の特徴を一緒くたにしてしまい、重要な情報が失われてしまう可能性があります。特にこのような複数センサーのデータの場合、実際に観測できるデータは ${\bf X} = {\bf A}{\bf Z}$ のように、潜在変数（信号源） ${\bf Z}$ の空間的な線形結合で表されることがしばしばあり、クラス分類において有用な情報はこの潜在変数に隠れていることも多いです（下図参照）。

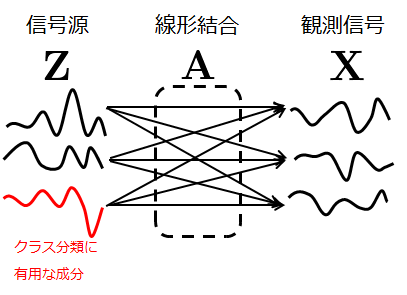
一方で、行列データとして直接扱うことの意味は、 ${\bf W} =\sum_{i = 1}^{r} \sigma_i {\bf u}_i {{\bf v}_i}^T$ と特異値分解して式（1）を以下のように変形すると見えてきます。

$\displaystyle a({\bf X}) = \sum_{i=1}^{r}(\sigma_i {{\bf u}_i}^T {\bf X} {\bf v}_i) + b \tag{2}$

このようにすると、 ${\bf u}$ は空間方向の特徴を抽出する空間フィルタ、 ${\bf v}$ は時間方向の特徴を抽出する時間フィルタとして考えることができ、時空間両方の特徴を捉えられることがわかります。上述のように観測されるデータが潜在変数の空間的な線形結合である場合にも、観測データに空間フィルタをかけることでクラス分類に有用な潜在的な情報を抽出した上で時間方向に係数をかけるので、時空間両方の特徴をとらえることができます。

行列データロジスティック回帰の目的関数

行列データの分類問題においてもロジスティック回帰は使えます。具体的には下記の誤差関数を最小化する ${\bf W}$ と $b$ を学習データ集合から求めればよいです。
$\displaystyle E({\bf W}, b) =-\sum_{i=1}^{N} \left\{y_i \ln \sigma({\rm Tr}({{\bf X}_i}^T {\bf W}) + b ) + (1 - y_i) \ln (1 - \sigma({\rm Tr}({{\bf X}_i}^T {\bf W}) + b )) \right\} \tag{3}$

トレースノルム正則化による低ランク化

さて、式（2）にあるように係数行列 ${\bf W}$ のランク $r$ が高いほど、かけ合わせる時空間フィルタの個数は増えます。もし、 ${\bf W}$ がフルランクなら $r = \min(D,T)$ 個の時空間フィルタをかけて重み付き和を取ることになります。しかし、上述のような潜在変数の中でもクラス分類に有用な情報は、（空間的に）ごく一部の成分でありそれ以外はノイズというケースも多くあります。例えば、上の図の例だと、3つの信号源のうちクラス分類に有用な成分は1つです。この場合に ${\bf W}$ がフルランクだと必要以上に複雑なモデルとなってしまい過学習となる恐れがあります。
ということで、 ${\bf W}$ を低ランクにしたいのですが、そのためにはこちらの記事で少し述べたトレースノルムの正則化項 $\|{\bf W} \|_{\rm trace}= \sqrt{{\rm Tr}({\bf W}^T {\bf W})}$ をつけると特異値がスパースになり、結果低ランクな解が得られます。具体的な式としては、
$\displaystyle F({\bf W}, b) =E({\bf W}, b) + \|{\bf W} \|_{\rm trace} \tag{4}$
であり、これを近接勾配法で解いていきます。なお、今回はバイアス項 $b$ は正則化の中に含めていないことに注意してください*1。 $b$ は正則化項に含まれないので、 ${\bf W}$ は近接勾配法の更新式、 $b$ は通常の勾配法の更新式で更新していきます。それぞれの更新式で必要な式（3）の ${\bf W}$ による微分および式（4）の $b$ による微分は、
$\displaystyle \nabla E({\bf W}) = \sum_{i=1}^{N} (\sigma({\rm Tr}({{\bf X}_i}^T {\bf W}) + b) - y_i) {\bf X}_i \tag{5}$
$\displaystyle \frac{ dF}{db} = \sum_{i=1}^{N} (\sigma({\rm Tr}({{\bf X}_i}^T {\bf W}) + b) - y_i) \tag{6}$
となるので、後はこれを元に ${\bf W}$ と $b$ の更新を交互に行えばよいです。

実装と実験

アルゴリズムの実装

今回の行列データロジスティック回帰は下記のように実装しました。基本的に今までと同じですが、proximal operatorはトレースノルム正則化のproximal operator計算を行うようにしており、近接勾配法の関数はバイアス項の更新（勾配法計算）も行うように変更しています。

import numpy as np
from numpy.random import *
import matplotlib.pyplot as plt
import sys

#ソフトしきい値作用素の計算
def soft_thresh(b, lam):
    x_hat = np.zeros(b.shape[0])
    x_hat[b >= lam] = b[b >= lam] - lam
    x_hat[b <= -lam] = b[b <= -lam] + lam
    return x_hat

#トレースノルム正則化のproximal operatorの計算
def prox_trace_norm(V, gamma, lam):
    [L, sig, R] = np.linalg.svd(V)
    sig_ = soft_thresh(sig, lam * gamma)
    if L.shape[1] > sig.shape[0]:
        L = L[:,:sig.shape[0]]
    if R.shape[1] > sig.shape[0]:
        R = R[:sig.shape[0], :]
    return np.dot(np.dot(L, np.diag(sig_)), R)

#近接勾配法とバイアス項の勾配法計算
def proximal_gradient_with_bias(grad_f, grad_b, prox, gamma, objective, init_x, init_b, tol = 1e-9):
    x = init_x
    b = init_b
    result = sys.maxint
    while 1:
        x_new = prox(x - gamma * grad_f(x, b), gamma)
        b_new = b - gamma * grad_b(x, b)
        result_new = objective(x_new, b_new)
        if result_new < tol or (np.abs(result - result_new)/np.abs(result) < tol) == True :
            break;
        x = x_new
        b = b_new
        result = result_new
    return x_new, b_new, result_new

#トレースノルム正則化項付きロジスティック回帰
#X:学習用データベクトルを列ベクトルとして並べた行列
#y:ラベルを並べたベクトル
def trace_norm_LogisticRegression(X, y, lam):
    sigma = lambda a : 1.0/(1.0+np.exp(-a))
    p=lambda Z, W, b:sigma(np.trace(np.dot(Z.T, W).T) + b) #メモ化したい・・・
    objective = lambda W, b: - np.sum( y * np.log(p(X, W, b)) +
                        (1 - y) *np.log(( 1 - p(X, W, b)))) + lam * np.linalg.norm(W, 'nuc')
    grad_E = lambda W, b: np.dot(X, p(X, W, b) - y) #勾配
    grad_b = lambda W, b: np.sum(p(X, W, b) - y)

    (u, l, v) = np.linalg.svd(X)
    Gamma =1.0/max(np.average(l.real*l.real,0)) 
    prox = lambda V, gamma:prox_trace_norm(V, gamma, lam) #proximal operator
    W_init = np.zeros((X.shape[0], X.shape[1]))
    b_init = 0
    (W, b, result) = proximal_gradient_with_bias(grad_E, grad_b, prox,
                                                    Gamma, objective, W_init, b_init, 1e-4)
    return W, b, result

なお、停止判定の方法については収束性を考慮して元の方法に戻しています。また、p(Z, W, b)の計算がかなり重いですが１回の更新で4回計算しているので、pをメモ化するなどの工夫を行えばもう少し速くできます（pの引数ZとWはnumpyのarray型なので簡単に辞書のキーにできず断念）。
あと、学習のステップ幅は今回かなりテキトーに決めた実装になっているので、その辺りはもう少し検討が必要です。

実験用疑似データ

実験用疑似のデータは下記のコードで生成しました。

    #学習データ
    #30×100の行列データ負例500個、正例500個
    #信号源のデータZ
    Z_train1=np.random.randn(30,100,500)
    Z_train2=np.random.randn(30,100,500)
    #30個の信号源のうち2個のみクラス分類に有用とする
    Z_train2[0, 20:50, :] += 0.2
    Z_train2[29, 80:90, :] -= 0.5
    Z_train = concatenate((Z_train1,Z_train2),2)

    #信号源データZを観測データに変換する行列A
    A = np.exp(-np.abs(np.tile(np.linspace(0, 1,30), (30,1)) -
            np.tile(np.linspace(0, 1,30), (30,1)).T)/0.1) + np.random.randn(30, 30)

    #実際に観測されるデータX
    X_train = np.dot(Z_train.T, A).T

    y_train1 = ones((500,1))
    y_train2 = zeros((500,1))
    y_train = concatenate((y_train1,y_train2),0).squeeze()

    #テストデータ
    #学習データと同じく30×100の行列データ負例500個、正例500個
    Z_test1=np.random.randn(30,100,500)
    Z_test2=np.random.randn(30,100,500)
    Z_test2[0, 20:50, :] += 0.2
    Z_test2[29, 80:90, :] -= 0.5
    Z_test = concatenate((Z_test1,Z_test2),2)

    X_test = np.dot(Z_test.T, A).T

    y_test1=ones((500,1))
    y_test2=zeros((500,1))
    y_test=concatenate((y_test1,y_test2),0).squeeze()

学習、テストに使用するデータはX_train、X_testですが、上述の信号源からの線形結合を模擬するため、まず潜在変数（信号源）Z_train、Z_testの生成を行いました。この信号源のデータは30成分ありますが、0番目の成分と29番目の成分のみがクラス分類に有用となるようなデータとしています。これを行列Aで線形結合して観測データXを生成しています。なお、行列Aは近くの信号程大きな重み、離れるほど小さな重みで足し合わせるような線形結合としており、更にこのAにもランダム成分を加えています。以下、正例・負例におけるXとZの平均波形を表示します。

y=1に対応する観測データ集合X_train1の平均波形

f:id:YamagenSakam:20180613230346p:plain

y=0に対応する観測データ集合X_train2の平均波形

f:id:YamagenSakam:20180613230616p:plain

y=1に対応する信号源データ集合Z_train1の平均波形

f:id:YamagenSakam:20180613230428p:plain

y=0に対応する信号源データ集合Z_train2の平均波形

f:id:YamagenSakam:20180613230713p:plain

やはり、観測データはy=0クラスとy=1クラスの平均データを見比べても、ノイズにまみれて差異があまり分からなくなっていますが、信号源データの場合は、2信号のみy=0クラスとy=1クラスで差異があることがはっきりわかります。

実験結果

このように生成した疑似データに対し、以下のコードのように $\lambda=0, 50, 100 \cdots, 2000$ と変化させて、その時の推定精度と $W$ のランクを求めてみました。

    num = 41
    scale = 50
    rank_of_W  = np.zeros(num)
    acc_arr = np.zeros(num)
    for i in range(0, num):
        (W, b, r) = trace_norm_LogisticRegression(X_train, y_train.squeeze(), i * scale)
        y_result = np.trace(np.dot(X_test.T, W).T) + b
        y_result[y_result>=0] = 1
        y_result[y_result<0] = 0
        rank_of_W[i] = np.linalg.matrix_rank(W)
        acc_arr[i] = np.sum(y_result == y_test)/float(y_test.shape[0])

その結果が以下の図です（赤が推定精度、青がランクです）。

f:id:YamagenSakam:20180613231839p:plain

L1ノルムロジスティック回帰と同様、 $\lambda$ を大きくしすぎても、制約がきつくなりすぎるのか精度が徐々に下がっていきます。実際今回の条件で推定精度が最大になったのは $\lambda = 1250$ のときで、精度が68.0%、 ${\bf W}$ のランクが4でした。以下には、この $\lambda = 1250$ での ${\bf W}$ を特異値分解して得られる空間フィルタ ${\bf U}$ を、y=0クラスのX_trainとy=1クラスのX_trainの平均行列に施した波形を示します。

y=1に対応する観測データ集合X_train1の平均に ${\bf U}$ をかけて得られる波形

f:id:YamagenSakam:20180613232012p:plain

y=0に対応する観測データ集合X_train2の平均に ${\bf U}$ をかけて得られる波形

f:id:YamagenSakam:20180613231951p:plain

この図の中で青の波形は最大特異値に対応する空間フィルタで抽出された波形、緑の波形は２番目に大きい特異値に対応する空間フィルタで抽出された波形です。この両者の注目すると、空間フィルタを施すことによって信号源に潜在しているクラス分類に有用な成分を抽出できていることがわかります。

まとめ

今回は行列データの分類アルゴリズムについて、ロジスティック回帰を例にとってトレースノルム正則化項によって低ランクな解が得られること、多次元の時系列データの分類問題などに有効であることを見てきました。トレースノルムの正則化は信号源の中でも一部の成分のみがクラス分類に有用であるとき特に威力を発揮します。
なお、時系列データの分類には今回紹介した方法以外にも隠れマルコフモデルを使った手法やリカレントニューラルネットワークの一種であるLong Short-Term Memory(LSTM)を使った手法もあります。特に最近は深層学習の流れもあってLSTMが主流になってきているとのことなので、そろそろニューラルネット辺りにも手を出していきたいところです。