はじめに
ここ1年くらい、ちまちまとatcoder中心に競技プログラミングに参加してたりします。ABCのD問題を解くのがやっとなのにAGCに突撃して爆死するってことを繰り返し続け、未だに緑コーダーです(パフォーマンスも1200前後がやっと)。こりゃまずいということで、もう少しまじめにアルゴリズムの勉強をしようと思い立ったので、今回から数回にわたって基本的なアルゴリズムのメモと実装を書いて、自分の理解を深めていこう思います。
今回はその中でも最短経路探索系(ダイクストラ法、ベルマン・フォード法、ワーシャル・フロイド法)のアルゴリズムについて書いていきます。これらのアルゴリズムについては、ネットや探せばいくらでも解説記事が出てくるので、ここでは主に自分が実装していく中で理解にしにくかった、ハマった点をポイントとして記していきます。そのため、ほぼ自分用のメモ&脳内整理用の記事なので、まじめな解説は他を当たった方が良いかもしれません。
ちなみに、今まで競プロも機械学習もpythonで実装してきましたが、今後本業でC++を使う機会が増えそうなので、今回はリハビリの意味も込めてC++での実装を行っていきます。
ダイクストラ法
用途
- 負のコストがない場合の単一始点最短経路探索。
アルゴリズムのポイント
- 始点に隣接している頂点からの順次最短経路を確定させていくアルゴリズム。
- 最短経路が確定した頂点に隣接する頂点と始点間のコストを計算・更新する処理を全部の頂点の最短経路が確定するまで繰り返す。
- 負のコストがない前提なので、現時点の始点からコスト計算されている頂点の中で最もコストが小さい頂点について、そのコストを最短経路として確定させてよい。
- 具体的には、始点の頂点のコストを0、それ以外の頂点までのコストを∞として初期化後、下記の処理を終了条件を満たすまで繰り返す。
- 最短経路が確定確定していない頂点の中からコストが最も小さい頂点を選択。
- その選択した頂点を最短経路確定頂点とする。
- その選択した頂点に隣接する頂点の現時点のコストが、選択した頂点へのコスト+辺のコストより大きければ、選択した頂点へのコスト+辺のコストに置き換える。
- 最短経路の復元のため、どの頂点から来たかも記憶しておき、最後にバックトラックで辿れるようにする。
実装のポイント
実装
メイン関数(呼び出し元)は省略。
#include <algorithm> #include <vector> #include <unordered_map> #include <queue> #include <functional> #include <climits> class edge { public: edge(int to, long long cost); int get_to() const; long long get_cost() const; private: int to; long long cost; }; edge::edge(int to, long long cost) : to(to), cost(cost) {} int edge::get_to() const { return to; } long long edge::get_cost() const { return cost; } class dykstra { private: //unordered_mapを使って隣接を構築 //first:接続元、second:辺のコストと接続先 std::unordered_map<int, std::vector<edge>> adj_list; int node_num; int start_point; std::vector<int> pred;//経路(遷移元)を保持 std::vector<long long> costs;//距離を保持 std::vector<bool> is_done;//確定ノードか否かを保持 public: dykstra(const int node_num, const std::unordered_map<int, std::vector<edge>>& adj_list); void calc_min_cost(int start); long long get_cost(int end) const; std::vector<int> get_min_path(int end) const; }; dykstra::dykstra(const int node_num, const std::unordered_map<int, std::vector<edge>>& adj_list) : adj_list(adj_list), start_point(0), node_num(node_num), pred(node_num + 1, INT_MAX), costs(node_num + 1, LLONG_MAX), is_done(node_num + 1, false) {} void dykstra::calc_min_cost(int start) { this->start_point = start; this->pred = std::vector<int>(node_num + 1, INT_MAX); this->costs = std::vector<long long>(node_num + 1, LLONG_MAX); this->is_done = std::vector<bool>(node_num + 1, false); //優先度付きキューpairで頂点番号と最短距離を保持 //firstの要素で比較されるので、firstが距離、secondを頂点番号とする std::priority_queue<std::pair<long long, int>, std::vector<std::pair<long long, int>>, std::greater<std::pair<long long, int>>> p_queue; p_queue.push(std::make_pair(0, start)); pred[start] = -1; costs[start] = 0; while (1) { if (p_queue.empty() == true) break; //キューが空なら終了 std::pair<long long, int> cost_node = p_queue.top(); p_queue.pop(); is_done[cost_node.second] = true; //キューから取り出した頂点を確定頂点とする for (auto &it : adj_list[cost_node.second]) { int adj_node = it.get_to(); if (is_done[adj_node] == false) { long long adj_cost = it.get_cost() + cost_node.first; if (adj_cost < costs[adj_node]) {//計算された隣接頂点のコストが現在のコストより小さいなら costs[adj_node] = adj_cost; //隣接頂点のコストを更新 pred[adj_node] = cost_node.second;//隣接頂点の遷移元を更新 p_queue.push(std::make_pair(adj_cost, adj_node));//キューに隣接頂点の情報を突っ込む } } } } } long long dykstra::get_cost(int end) const { return costs[end]; } std::vector<int> dykstra::get_min_path(int end) const { int node = end; std::vector<int> vec; vec.push_back(node); //終点から始点までの経路をたどる while (1) { //始点から辿れない頂点or //始点であれば終了 if (pred[node] >= INT_MAX || pred[node] == -1) break; node = pred[node]; vec.push_back(node); } std::reverse(vec.begin(), vec.end()); return vec; }
AOJのALDS1_12_Cが通ることを確認。
ベルマン・フォード法
用途
- 負のコストがある場合の単一始点最短経路探索および負のサイクル検出。
アルゴリズムのポイント
- 全ての辺のコストを見て、各頂点までの最短経路(コスト)を更新するという処理を所定の回数繰り返すアルゴリズム。
- 具体的には、始点の頂点のコストを0、それ以外の頂点までのコストを∞として初期化後、下記の処理を所定の回数繰り返す(回数については後述)。
- 各辺に対して、接続元の頂点のコスト+辺のコストが接続先の頂点のコストより小さければ、接続先頂点のコストを接続元の頂点のコスト+辺のコストに置き換える。
- この処理を全ての辺に対して行う。
- 負のサイクルがあれば、始点からの最短経路は全ての頂点に対して求まらない(いくらでもコストを小さくできるので)。
- 頂点数をVとして、負のサイクルがグラフ上にない場合、始点から各頂点までの最短経路の経由頂点数は高々V-1個(始点は除く)。
- これらのことから負のサイクルがなければ、V-1回の繰り返しで全頂点までの最短経路が求まる。逆にV回目に更新が発生するのならばグラフに負のサイクルがあると判定可能。
- 更に、V~V*2回目の繰り返しにおいて、最短経路が更新される頂点は負のサイクルに含まれると判断される。
- 加えて、負のサイクルに含まれていると確定している頂点から辿れる頂点についても、負のサイクルに含まれる頂点。
- 上記のことより、特定終点までの最短経路と負のサイクルの有無を求める場合は、全頂点の最短経路更新および負のサイクル情報の伝搬処理をV*2回繰り返す(グラフ全体に負のサイクルがあるか否かを求めるだけの場合はV回の繰り返しでよい)。
実装のポイント
実装
#include <algorithm> #include <vector> #include <unordered_map> #include <functional> #include <climits> class edge { public: edge(int to, long long cost); int get_to() const; long long get_cost() const; private: int to; long long cost; }; edge::edge(int to, long long cost) : to(to), cost(cost) {} int edge::get_to() const { return to; } long long edge::get_cost() const { return cost; } class bellman_ford { private: //unordered_mapを使って隣接グラフを構築 //first:接続元、second:辺のコストと接続先 std::unordered_map<int, std::vector<edge>> adj_list; int node_num; int start_point; std::vector<int> pred;//経路(遷移元)を保持 std::vector<long long> costs;//距離を保持 bool is_negative_graph;//グラフ内に負のサイクルをもつか否か std::vector<bool> is_negative_pass;//経路上に負のサイクルを持つか否か public: bellman_ford(const int node_num, const std::unordered_map<int, std::vector<edge>>& adj_list); void calc_min_cost(int start); long long get_cost(int end) const; bool get_is_negative_graph() const; std::vector<int> get_min_path(int end) const; }; bellman_ford::bellman_ford(const int node_num, const std::unordered_map<int, std::vector<edge>>& adj_list) : adj_list(adj_list), start_point(0), node_num(node_num), pred(node_num + 1, INT_MAX), costs(node_num + 1, LLONG_MAX), is_negative_graph(false), is_negative_pass(node_num + 1, false) {} void bellman_ford::calc_min_cost(int start) { this->start_point = start; this->pred = std::vector<int>(node_num + 1, INT_MAX); this->costs = std::vector<long long>(node_num + 1, LLONG_MAX); this->is_negative_pass = std::vector<bool>(node_num + 1, false); pred[start] = -1; costs[start] = 0; for (int i = 0; i < 2 * node_num; i++) { for (auto &node : adj_list) { if (costs[node.first] == LLONG_MAX) continue; for (auto &adj : adj_list[node.first]) { int adj_node = adj.get_to(); long long adj_cost = adj.get_cost() + costs[node.first]; if (adj_cost < costs[adj_node]) {//計算された隣接頂点のコストが現在のコストより小さいなら costs[adj_node] = adj_cost;//隣接頂点のコストを更新 pred[adj_node] = node.first;//隣接頂点の遷移元を更新 if (i >= node_num - 1) { //頂点数回以上繰り返しても、 //まだ更新が発生するなら、その頂点への経路には負のサイクルあり is_negative_pass[adj_node] = true; is_negative_graph = true; } } if (is_negative_pass[node.first] == true) {//負のサイクル情報伝搬 //経路に負のサイクルを含む頂点に連結されているなら、 //その頂点への経路も負のサイクルを含む is_negative_pass[adj_node] = true; } } } } } bool bellman_ford::get_is_negative_graph() const { return is_negative_graph; } long long bellman_ford::get_cost(int end) const { if (is_negative_pass[end] == false) return costs[end]; else return LLONG_MIN; } std::vector<int> bellman_ford::get_min_path(int end) const { int node = end; std::vector<int> vec; vec.push_back(node); //終点から始点までの経路をたどる while (1) { //負のサイクルを含む頂点or //始点から辿れない頂点or //始点であれば終了 if (is_negative_pass[node] == true || pred[node] >= INT_MAX || pred[node] == -1) break; node = pred[node]; vec.push_back(node); } std::reverse(vec.begin(), vec.end()); return vec; }
AOJのGRL_1_Bが通ることを確認。加えて、グラフそのものに負のサイクルを含むか否かではなく、目的の経路に負サイクルがあるかという判定が正しく動作するか検証するために、atcoderのABC061Dでも確認。
ワーシャル・フロイド法
用途
- 全頂点ペアの最短経路探索。
- 負のコストがあっても良く、負のサイクル検出も可能。
アルゴリズムのポイント
- 頂点iから頂点jへ頂点0~k-1のみを経由する最短経路が既に得られているとして、それに頂点kを追加して最短経路を更新していくという動的計画法の一種。
- もし頂点kを追加してi→j間の最短経路更新が発生するということは、更新後のi→jの最短経路はi→kの最短経路+k→jの最短経路。
- 従って、i→kの最短経路のコスト+k→jの最短経路のコストが、既に得られているi→jへの最短経路のコストよりも小さければ更新。
- 具体的には頂点iから頂点jへの最短経路のコストをcost[i][j]とし、隣接行列で初期化した後、以下の処理を行う。
- k =0~Vに対し、以下の処理を繰り返す。
- 全頂点のペアi, jについて、既に得られている0~k-1のみを経由する最短経路cost[i][j]よりもcost[i][k] + cost[k][j]が小さければ、頂点kを追加することで経路が更新されるということなので、cost[i][j]をcost[i][k] + cost[k][j]に置き換える。
- 上記処理完了後、costの対角成分(自分から自分への距離)が負ならば、そのグラフには負のサイクルがあり、その頂点は負のサイクルに含まれる。
- 対角成分が負でなくても、負のサイクルに含まれる頂点から辿れる頂点も負のサイクルに含まれる。
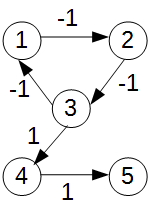
上記の方法で、各頂点が負のサイクルに含まれるか判断可能なので、頂点iから頂点jへの経路に負のサイクルを含むか否かは、終点jが負のサイクルに含まれるか否かで判断可能(この辺り、あまり文献が見つからず自分で考えたので少し怪しい)。やっぱり間違えてる(というより処理が足りない)。以下のようなグラフで、4→5は負のサイクルを含まないのに、負のサイクルありと判定されてしまう。ちゃんと伝搬元の負のサイクルに含まれる頂点が始点iから辿れるか?も判断しないといけない(時間がないのでコードの修正は別途)。
実装のポイント
- k=0~V、i=0~V、j=0~Vの3重ループを回す。
- アルゴリズムの性質上、グラフの表現には隣接行列を採用。
- 隣接行列の未接続の表現にLLONG_MAXを使っているので、呼び出し元は注意が必要。
実装
#include <algorithm> #include <vector> #include <functional> #include <climits> class warshall_floyd { private: int node_num; bool is_negative_graph; std::vector<std::vector<long long>> cost_matrix;//隣接行列を構築 std::vector<std::vector<int>> pred;//経路(遷移元)を保持 public: warshall_floyd(const int node_num, const std::vector<std::vector<long long>> &adj_matrix); bool get_is_negative_graph() const; bool get_is_negative_pass(int start, int end) const; long long get_cost(int start, int end) const; std::vector<int> get_min_path(int start, int end) const; }; warshall_floyd::warshall_floyd(const int node_num, const std::vector<std::vector<long long>> &adj_matrix): cost_matrix(adj_matrix), node_num(node_num), is_negative_graph(false), pred(node_num + 1, std::vector<int>(node_num + 1, INT_MAX)) { //predの初期化 for (int i = 0; i <= node_num; i++) { for (int j = 0; j <= node_num; j++) { if (i == j) pred[i][j] = -1; else if (adj_matrix[i][j] < LLONG_MAX) { pred[i][j] = i; } } } //ワーシャルフロイドの更新式 for (int k = 0; k <= node_num; k++) { for (int i = 0; i <= node_num; i++) { for (int j = 0; j <= node_num; j++) { if (cost_matrix[i][k] < LLONG_MAX && cost_matrix[k][j] < LLONG_MAX) { if (cost_matrix[i][k] + cost_matrix[k][j] < cost_matrix[i][j]) { cost_matrix[i][j] = cost_matrix[i][k] + cost_matrix[k][j]; //経路復元用 //pred[i][j]にはi→jの最短経路におけるjの1つ前の頂点が入る。 //pred[k][j]にはk→jの最短経路におけるjの1つ前の頂点が入っている。 //この処理を通るということは最短経路がkを使った経路に変わる //ということでありi→jへの経路の中にk→jの最短経路を含むことになる。 //従って新しいi→jにおけるjの1つ前の頂点は //k→jにおけるjの1つ前の頂点、すなわちpred[k][j]となる。 pred[i][j] = pred[k][j]; } } } } } //負のサイクル検出 //[注意!]間違っているので修正必要!(アルゴリズムのポイントを参照) for (int i = 0; i <= node_num; i++) { //自分への距離が負になるならその頂点は負のサイクルに含まれる if (cost_matrix[i][i] < 0) { for (int j = 0; j <= node_num; j++) { //負のサイクルに含まれる頂点から辿れる頂点も負のサイクルになる if (i == j) continue; if (cost_matrix[i][j] < LLONG_MAX && cost_matrix[j][j] >= 0) cost_matrix[j][j] = -1; } is_negative_graph = true; //break; } } } bool warshall_floyd::get_is_negative_graph() const { return is_negative_graph; } bool warshall_floyd::get_is_negative_pass(int start, int end) const { //startからendにたどり着けない場合はfalseを返す if (cost_matrix[start][end] < LLONG_MAX) { //startからend辿りつける場合、 //endが負のサイクルに含まれるならtrueを返す if (cost_matrix[end][end] < 0) return true; } return false; } long long warshall_floyd::get_cost(int start, int end) const { return cost_matrix[start][end]; } std::vector<int> warshall_floyd::get_min_path(int start, int end) const { int node = end; std::vector<int> vec; vec.push_back(node); //終点から始点までの経路をたどる while (1) { //負のサイクルを含む頂点or //始点から辿れない頂点or //始点であれば終了 if (cost_matrix[node][node] < 0 || pred[start][node] >= INT_MAX || pred[start][node] == -1) break; node = pred[start][node]; vec.push_back(node); } std::reverse(vec.begin(), vec.end()); return vec; }
AOJのGRL_1_Cが通ることを確認。後、負サイクル検出ロジックの検証のため、上記同様atcoderのABC061Dも確認(ワーシャル・フロイドで解くには少しきつい問題設定だけどC++なら通る)。
おわりに
今回は、競プロレベルアップに向け最短経路探索系アルゴリズムに関するメモと実装を書きました。
ただ、ここに書いたコードがそのまま競プロに使えるケースはあまりないと思います。例えば、ダイクストラ法を使うにしても、辺のコストがあらかじめ与えられておらず(もしくは与えようとすると膨大なメモリ使用量になる等)キューから取り出して、コスト計算時に初めて辺のコストがわかるなんて問題もあります。そんな問題だとここに書いた実装はそのまま使えないので、カスタマイズする必要があります。
あとそのまま使えるにしても、問題文からはそのことがパッとわからない、または、アルゴリズムを使うのはわかるけどどうやって適用するかを考える必要がある(問題で与えられたコストを負値にする、スタートとゴール両方から計算する、等々)なんてこともあります。その辺りの考察力が勝負になってくる世界なので、強化するべきはそこなんだと思いますが、まずは基本を理解しないと考察力も鍛えられないかなと
ということで、次回以降はその他のグラフアルゴリズム(幅優先、深さ優先、最小全域木とか)、探索系(二分探索、尺取り法とか)、数学系(素数、modとか)、動的計画法辺りを書いていこうと思います。