ベイズ推論による教師あり分類～ガウス混合分布編～

はじめに

以前、ベイズ推論による機械学習入門という書籍を読み、以下のような記事を公開しました。

yamagensakam.hatenablog.com

この書籍には、多次元ガウス混合モデルによるクラスタリング手法が詳しく述べられていますが、多次元ガウス混合モデルによる教師あり分類の手法は少し触れる程度にとどまっています（クラスタリングで述べられている導出過程を流用すれば、比較的簡単に導出できるためだと思います）。
ということで、今回は多次元ガウス混合モデルによる教師あり分類の導出、実装をやってみました。

ガウス混合モデル

モデル自体は教師ありだろうが、教師なしだろうが同じモデルを考えることができます。まず、全て独立でサンプリングされる $D$ 次元のデータが ${\bf X} = \left\{ {\bf x}_1 , \cdots, {\bf x}_N \right\}$ と $N$ 個あるとし、そのそれぞれに対応するラベルデータを ${\bf S} = \left\{ {\bf s}_1 , \cdots, {\bf s}_N \right\}$ とします。ここで、 ${\bf s}$ は $1$ of $K$ 表現と呼ばれ、クラス数が $K$ の場合、所属するクラスに対応する要素のみ $1$ で他は全て $0$ の $K$ 次元ベクトルです。この ${\bf s}$ をサンプルするための分布として、パラメータ ${\bf \pi}$ を持つカテゴリ分布を考えます。
また、 $K$ 個のガウス分布が混合したモデルを考えるので、それぞれの分布の平均を ${\bf \mu}_1, \cdots, {\bf \mu}_K$ 、精度行列（共分散行列の逆行列）を ${\bf \Lambda}_1,\cdots, {\bf \Lambda}_K$ とします。なお、各パラメータを個別に扱わない場面では表記を簡単にするため、これらのガウス混合分布のパラメータを全てまとめて ${\bf \Theta}$ と表記します。
更に、カテゴリ分布のパラメータ ${\bf \pi}$ や各ガウス分布の ${\bf \mu}_k$ 、 ${\bf \Lambda}_k$ といったパラメータもベイズ推論の枠組みでは、確率分布に従うと考えます。ここでは、それぞれ共役事前分布に従うことにします。具体的には、

$\displaystyle p({\bf \pi}) = {\rm dir}({\bf \pi} | {\bf \alpha}) \tag{1}$
$\displaystyle p({\bf \mu}_k, {\bf \Lambda}_k) = {\rm NW} ({\bf \mu}_k, {\bf \Lambda}_k | {\bf m}, \beta, \nu, {\bf W} ) \tag{2}$

という分布に従うとします。ここで、 ${\rm dir}(\cdot)$ はディリクレ分布、 ${\rm NW}(\cdot)$ はガウス・ウィシャート分布です（具体的な分布の式は書籍を参照ください）。ここで事前分布として共役事前分布を採用しておくと事後分布や予測分布が解析的に求めることができます。 ${\bf \alpha}$ や ${\bf m}, \beta, \nu, {\bf W}$ は超パラメータで今回は事前に与えるものとします。また、 ${\bf m}, \beta, \nu, {\bf W}$ については、それぞれのガウス分布で異なる値を与えることもできますが、簡単のため今回は全て共通の値とします。
さて、ここまで出てきた確率変数 ${\bf X}, {\bf S}, {\bf \pi}, {\bf \Theta}$ の同時分布を考えると、以下のようになります。
${ \displaystyle \begin{eqnarray} p({\bf X}, {\bf S}, {\bf \pi}, {\bf \Theta}) &=& p({\bf X} | {\bf S}, {\bf \Theta}) p ({\bf S}|{\bf \pi})p({\bf \Theta})p({\bf \pi} ) \\ &=& \left\{\prod_{i = 1}^{N} \prod_{k = 1}^{K} {\rm N}({\bf x}_i| {\bf \mu}_k, {\bf \Lambda}_k^{-1})^{{\bf s}_{i, k}} {\rm Cat}({\bf s}_k | {\bf \pi})\right\} \left\{ \prod_{k = 1}^{K} p({\bf \mu}_k, {\bf \Lambda}_k) \right\} p({\bf \pi}) \end{eqnarray} } \tag{3}$

ここで、 ${\rm N}(\cdot)$ はガウス分布、 ${\rm Cat}(\cdot)$ はカテゴリ分布を表し、 $p({\bf \pi})$ と $p({\bf \mu}_k, {\bf \Lambda}_k)$ は式（1）、式（2）で表される分布です。
このモデルのグラフィカルモデルを下図に示します。この図で ${\bf X}$ と ${\bf S}$ の四角で囲まれているのが学習データとして与えられるデータ、 ${\bf x}_*$ と ${\bf s}_*$ がクラスを予測する対象のデータ（テストデータ）です。

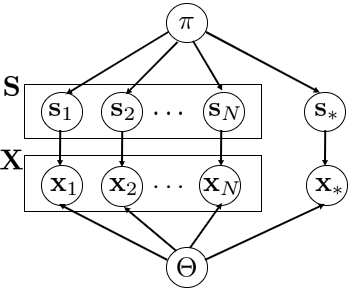
このように図示しておくと有効分離の考え方を用いて、変数間の条件付き独立性がわかりやすくなり、後々式展開する際に便利です。有効分離については、以下の記事がわかりやすいと思います。

条件付き独立と有向分離を用いた統計モデルの妥当性チェック - StatModeling Memorandum

推論

上述式（3）のモデルから、パラメータの事後分布とそれを元に、新たなデータ ${\bf x}_*$ が与えられた時の ${\bf s}_*$ の確率分布である予測分布を導出します。このモデルの場合、上述のように共役事前分布を事前分布として採用しているため、事後分布および予測分布は解析的に求めることができます。ここでは、逐次的にデータが与えられるとして、オンラインで予測分布を更新していけるような式を導出します。

事後分布の導出

今回扱う問題では ${\bf X}$ と ${\bf S}$ がデータとして与えられるので、これらが与えられている下でのパラメータの事後分布を求めます。つまり、

$\displaystyle p({\bf \Theta}, {\bf \pi}|{\bf X}, {\bf S}) = \frac{p({\bf X}, {\bf S}, {\bf \pi}, {\bf \Theta})}{p({\bf X}, {\bf S})} \varpropto p({\bf X}, {\bf S}, {\bf \pi}, {\bf \Theta}) \tag{4}$

を求めることになります。なお、クラスタリングの場合、 ${\bf S}$ がデータとして与えられているわけではないので、求めるべき事後分布としては $p({\bf \Theta}, {\bf \pi}, {\bf S}|{\bf X})$ となり、こちらは解析的に求めることが難しくなります（なので、ギブスサンプリングや変分推論などの近似手法を使う）。
ここで式（3）を見ると、 $\Theta$ と $\pi$ は完全に分離していることがわかります。つまり、 ${\bf X}$ と ${\bf S}$ が与えられた下では、 $\Theta$ と $\pi$ は独立であり、

$\displaystyle p({\bf \Theta} |{\bf X}, {\bf S}) \varpropto p({\bf X} | {\bf S}, {\bf \Theta})p({\bf \Theta}) \tag{5}$
$\displaystyle p({\bf \pi} |{\bf X}, {\bf S}) =p({\bf \pi} |{\bf S}) \varpropto p ({\bf S}|{\bf \pi})p({\bf \pi} ) \tag{6}$

を求めればよいことになります。
それでは、式（5）を展開してみます。式（5）の右辺について、対数をとってみると、

${ \displaystyle \begin{eqnarray} \ln p({\bf X} | {\bf S}, {\bf \Theta}) p({\bf \Theta}) &=& \ln \prod_{i = 1}^{N} \prod_{k = 1}^{K} {\rm N}({\bf x}_i| {\bf \mu}_k, {\bf \Lambda}_k^{-1})^{{\bf s}_{i, k}} p({\bf \mu}_k, {\bf \Lambda}_k)\\ &=& \sum_{k = 1}^{K} \left\{ \sum_{i = 1}^{N} s_{i,k} \ln {\rm N}({\bf x}_i| {\bf \mu}_k, {\bf \Lambda}_k^{-1}) + {\rm NW} ({\bf \mu}_k, {\bf \Lambda}_k | {\bf m}, \beta, \nu, {\bf W} ) \right\} \end{eqnarray} } \tag{7}$

となります。これを見ると各 $k$ に対して分離しているのがわかるので、各 $k$ に対し ${\bf \mu}_k, {\bf \Lambda}_k$ それぞれ独立に事後分布を求めればよいことになります。また、式（7）の中括弧の中はガウス・ウィシャート分布を事前分布として用いたガウス分布パラメータの事後分布推定の計算となります。この計算方法は件の書籍に詳しく載っているので、ここでは割愛しますが、最終的な形は以下のようになります。
$\displaystyle p({\bf \mu}_k, {\bf \Lambda}_k | {\bf X}, {\bf S}) = {\rm WA}({\bf \mu}_k, {\bf \Lambda}_k | \hat{{\bf m}}_k, {\hat \beta}_k, {\hat \nu}_k, {\hat {\bf W}}_k) \tag{8}$
ただし、

${ \displaystyle \begin{eqnarray} {\hat \beta}_{k} &=& \sum_{i = 1}^{N} s_{i, k} + \beta \\ {\hat \nu}_{k} &=& \sum_{i = 1}^{N} s_{i, k} + \nu \\ {\hat {\bf m}}_{k} &=& \frac{\sum_{i = 1}^{N} s_{i, k} {\bf x}_{i} + \beta {\bf m} } {{\hat \beta}_{k}} \\ {\hat {\bf W}}_{k} ^{-1} &=& \sum_{i = 1}^{N} s_{i, k} {\bf x}_{i} {\bf x}_{i}^T + \beta {\bf m}{\bf m}^T - {\hat \beta}_{k}{\hat {\bf m}}_{k} {\hat {\bf m}}_{k}^{T} + {\bf W}^{-1}\\ \end{eqnarray} } \tag{9}$

です。同様に式（6）はディリクレ分布を事前分布としてカテゴリ分布の事後分布そのものであるため、

$\displaystyle p({\bf \pi} |{\bf S}) = {\rm dir}({\bf \pi}| {\hat {\bf \alpha}}) \tag{10}$

というディリクレ分布になります。ただし、

$\displaystyle \alpha_{k} = \sum_{i = 1}^{N} s_{i, k} + \alpha \tag{11}$

です。

ここで、式（9）および式（11）の各超パラメータをデータが与えられるたびに逐次更新できる形に変更すると、

${ \displaystyle \begin{eqnarray} {\hat \beta}_{n, k} &=& {\hat \beta}_{n-1, k} + s_{n, k} \\ {\hat \nu}_{n, k} &=& {\hat \nu}_{n-1, k} + s_{i, k} \\ {\hat {\bf m}}_{n, k} &=& \frac{s_{n, k} {\bf x}_{n} + {\hat \beta}_{n-1, k} {\hat {\bf m}}_{n-1, k} } {{\hat \beta}_{n, k}}\\ {\hat {\bf W}}_{n, k}^{-1} &=& { \hat {\bf W}}_{n-1, k}^{-1} + s_{i, k}{\bf x}_{i} {\bf x}_{i}^T +{\hat \beta}_{n-1, k}{\hat {\bf m}}_{n-1, k} {\hat {\bf m}}_{n-1, k}^{T} - {\hat \beta}_{n, k}{\hat {\bf m}}_{n, k} {\hat {\bf m}}_{n, k}^{T} \\ {\hat \alpha}_{n, k} &=& {\hat \alpha}_{n-1, k} + s_{i, k} \end{eqnarray} } \tag{12}$

となり、これにより $n-1$ の時点で、計算した超パラメータを用いて、 $n$ 番目のデータが来たときの超パラメータに更新することが可能です（初期値は事前分布の超パラメータ ${\bf m}, \beta, \nu, {\bf W}, \alpha$ ）。

予測分布の導出

最終的に欲しいのは、新たなデータ ${\bf x}_*$ が与えられた時のクラス分類結果 ${\bf s}_*$ です。そのため、 ${\bf x}_*$ が与えられた下での ${\bf s}_*$ の予測分布を求めます。予測分布は、

$\displaystyle p({\bf s}_* | {\bf x}_*, {\bf X}, {\bf S} ) = \frac{p({\bf s}_* , {\bf x}_*, {\bf X}, {\bf S} )}{p( {\bf x}_*, {\bf X}, {\bf S} )} = \frac{p({\bf x}_*| {\bf s}_* , {\bf X}, {\bf S} )p( {\bf X}|{\bf s}_*, {\bf S})p({\bf s}_*|{\bf S})p({\bf S})}{{p( {\bf x}_*, {\bf X}, {\bf S} )}} \tag{13}$

となります。ここで、 ${\bf s}_*$ に関係のない項は無視していいので、 $p({\bf S})$ と $p( {\bf x}_*, {\bf X}, {\bf S} )$ は考慮から外します。更に、 $p( {\bf X}|{\bf s}_*, {\bf S})$ について、グラフィカルモデルから有効分離性を読み解くと ${\bf S}$ が与えられた下では、 ${\bf X}$ と ${\bf s}_*$ は独立であり（ ${\bf X}$ に繋がる ${\bf S}$ が観測され、かつ、head-to-head型を形成している ${\bf s}_*, {\bf x}_*, {\bf \Theta}$ において ${\bf x}_*$ が観測されていないため）、 $p( {\bf X}|{\bf s}_*, {\bf S})= p( {\bf X}| {\bf S})$ となるため、こちらも考慮しなくてよくなります。まとめると、式（13）は

$\displaystyle p({\bf s}_* | {\bf x}_*, {\bf X}, {\bf S} ) \varpropto p({\bf x}_*| {\bf s}_* , {\bf X}, {\bf S} ) p({\bf s}_*|{\bf S}) \tag{14}$

と、2つの項のみ考えればよくなります。1つ目の項は、
$\displaystyle p({\bf x}_*| {\bf s}_* , {\bf X}, {\bf S} ) = \int p({\bf x}_* | {\bf s}_* ,{\bf X},{\bf S}, {\bf \Theta} ) p({\bf \Theta}| {\bf s}_*,{\bf X},{\bf S}) d {\bf \Theta} \tag{15}$

であり、ここでもグラフィカルモデルから有効分離性を考えると $p({\bf x}_* | {\bf s}_* ,{\bf X},{\bf S}, {\bf \Theta} ) =p({\bf x}_* | {\bf s}_* , {\bf \Theta} )$ 、 $p({\bf \Theta}| {\bf s}_*,{\bf X},{\bf S}) = p({\bf \Theta}| {\bf X},{\bf S})$ とすることができます。従って、

$\displaystyle p({\bf x}_*| {\bf s}_* , {\bf X}, {\bf S} ) = \int p({\bf x}_* | {\bf s}_* , {\bf \Theta} ) p({\bf \Theta}| {\bf X},{\bf S}) d {\bf \Theta} \tag{16}$

となります。
$p({\bf \Theta}| {\bf X},{\bf S})$ は、式（5）、式（8）、式（9）に記している事後分布そのものです。今、各 $k$ に対して ${s}_{*,k} = 1$ であるそれぞれの予測分布を求めたいので、式（16）より

$\displaystyle p({\bf x}_*| {\bf s}_{*,k} = 1 , {\bf X}, {\bf S} ) = \int \int p({\bf x}_* | {\bf \mu}_k, {\bf \Lambda}_k ) p({\bf \mu}_k, {\bf \Lambda}_k | {\bf X},{\bf S}) d {\bf \mu}_k d {\bf \Lambda}_k \tag{17}$

を求めればよいことになります。これは、ガウス・ウィッシャート分布を事前分布として用いた場合のガウス分布の予測分布計算になります。こちらも予測分布導出は書籍に載っているので、導出過程は省略し最終形を示します。

$\displaystyle p({\bf x}_*| {\bf s}_{*,k} = 1 , {\bf X}, {\bf S} ) = {\rm St}({\bf x}_* |{\hat {\bf m}}_{n, k}, \frac{(1-D+ {\hat \nu}_{n, k}){\hat \beta}_{n, k} }{1 + {\hat \beta}_{n, k} } {\hat {\bf W}}_{n,k}, 1-D+ {\hat \nu}_{n, k}) \tag{18}$

ただし、 ${\rm St}(\cdot)$ は多次元のスチューデントのt分布で、 $D$ は ${\bf x}$ の次元です。
次に、式（14）の $p({\bf s}_*|{\bf S})$ ですが、こちらも同様に、

$\displaystyle p({\bf s}_*|{\bf S}) = \int p({\bf s}_*|{\bf S},{\bf \pi})p({\bf \pi}| {\bf S}) d {\bf \pi} = \int p({\bf s}_*|{\bf \pi})p({\bf \pi}| {\bf S}) d {\bf \pi} \tag{19}$

となります。ただし、第2式から第3式への展開はグラフィカルモデルより ${\bf \pi}$ を観測した下での ${\bf S}$ と ${\bf s}_*$ の条件付き独立性を利用しました。そしてこの式（19）は、ディリクレ分布を事前分布として使ったカテゴリ分布の予測分布です。ということで、この予測分布についても導出過程は割愛し最終形を示します。

$\displaystyle p({\bf s}_*|{\bf S}) = {\rm Cat}({\bf s}_*|{\hat {\bf \eta}}_{n}) \tag{20}$

ただし、 ${\hat {\bf \eta}_{n}}$ の各要素 ${\hat \eta}_{n,k}$ は
$\displaystyle {\hat \eta}_{n,k}= \frac{{\hat \alpha}_{n, k}}{\sum_{i=1}^K {\hat \alpha}_{n, i}} \tag{21}$
です。
ここまでの話をまとめると、 $n$ 番目のデータが与えら手た時の予測分布の更新式は、式（14）、式（17）、式（20）、式（21）より

$\displaystyle p(s_{*, k} = 1 | {\bf x}_*, {\bf X}, {\bf S} ) \varpropto {\hat \eta}_{n,k} {\rm St}({\bf x}_* |{\hat {\bf m}}_{n, k}, \frac{(1-D+ {\hat \nu}_{n, k}){\hat \beta}_{n, k} }{1 + {\hat \beta}_{n, k} } {\hat {\bf W}}_{n,k}, 1-D+ {\hat \nu}_{n, k}) \tag{22}$

となります（各超パラメータは式（12）、式（21））。そして、各クラスの所属確率の平均を得たいときは、 $k = 1 \cdots K$ に対し、式（22）の右辺に ${\bf x}_*$ を代入し、得られる値を合計が1になるように正規化すればよいです。

実装

ということで実装です。

import numpy as np
import scipy as sci
import math
import random
import matplotlib.pyplot as plt
import matplotlib.animation as anm

class multivariate_student_t():
    def __init__(self, mu, lam, nu):
        self.D   = mu.shape[0]
        self.mu  = mu
        self.lam = lam
        self.nu  = nu

    def pdf(self, x):
        temp1 = np.exp( math.lgamma((self.nu+self.D)/2) - math.lgamma(self.nu/2) )
        temp2 = np.sqrt(np.linalg.det(self.lam)) / (np.pi*self.nu)**(self.D/2)
        temp3 = 1 + np.dot(np.dot((x-self.mu), self.lam),  (x-self.mu))/self.nu
        temp4 = -(self.nu+self.D)/2
        return temp1*temp2*((temp3)**temp4)

class mixture_gaussian_classifier:
    def __init__(self, alpha0, m0, invW0, beta0, nu0):
        self.K = alpha0.shape[0]

        #予測分布（多次元t分布）の生成
        self.pred_distr = (lambda m, W, beta, nu:
                                      multivariate_student_t
                                      (m,
                                      (1 - m.shape[0] + nu) * beta * W/(1 + beta),
                                      (1 - m.shape[0] + nu)))

        #超パラメータの初期化
        self.alpha = alpha0
        self.eta = alpha0/np.sum(alpha0)
        self.m = [None] * self.K
        self.invW = [None] * self.K
        self.beta = np.zeros(self.K)
        self.nu = np.zeros(self.K)
        for k in range(self.K):
            self.m[k] = m0
            self.invW[k] = invW0
            self.beta[k] = beta0
            self.nu[k] = nu0



    def train(self, x, s):
        #各超パラメータの更新
        k = np.where(s == 1)[0][0]
        self.alpha[k] += 1.0
        self.eta = self.alpha/np.sum(self.alpha)
        pre_beta = self.beta[k]
        self.beta[k] += 1.0
        self.nu[k] += 1.0
        pre_m = self.m[k]
        self.m[k] = (x + pre_m * pre_beta)/self.beta[k]
        self.invW[k] = (self.invW[k] + np.dot(x.reshape(-1,1), x.reshape(-1,1).T)
                        - self.beta[k] * np.dot(self.m[k].reshape(-1,1), self.m[k].reshape(-1,1).T)
                        + pre_beta * np.dot(pre_m.reshape(-1,1), pre_m.reshape(-1,1).T))

    def test(self, x):
        s = np.zeros(self.K)
        #各クラスの予測平均を算出
        for k in range(self.K):
            s[k] = (self.eta[k] *
                    self.pred_distr(self.m[k], np.linalg.inv(self.invW[k]),
                                    self.beta[k], self.nu[k]).pdf(x))
        s /= np.sum(s)
        return s

クラスmixture_gaussian_classifierは、ここまで述べてきた学習（train）と予測平均の算出（test）を行うクラスです。また、multivariate_student_t多次元のスチューデントのt分布のクラスで、この実装については、以下の記事の内容を参考にさせてもらいました。

<ベイズ推論> 多次元ガウス分布の学習 - Helve’s Python memo

実験・結果

ということで、以下のようなコードを組んで実験してみました。クラス数は $K=3$ で、学習データ数はそれぞれ $N_1=50, N_2 = 60, N_3 = 70$ と少し偏りを持たせています。
また、せっかく事後分布を逐次学習できるようにしたので、学習データが与えられるたびに予測平均がどのように変化するかをアニメーションにしてみました。

global used_idx

def update(i, idx, mgc, X, S):
    plt.cla
    test_range = range(0,60)
    X_new = np.zeros((2, len(test_range)**2))
    S_new = np.zeros((3, len(test_range)**2))
    i = idx[i]

    #データの学習
    mgc.train(X[:, i],S[:, i])

    used_idx.append(i)
    c = S[:, used_idx]

    plt.scatter(X[0, used_idx], X[1, used_idx],
                edgecolors="black", marker="o" , color=S[:, used_idx].T)

    count = 0
    S_res = np.zeros((len(test_range), len(test_range), 3))
    for x1 in test_range:
        for x2 in test_range:
            #各座標位置に対する予測平均を算出
            X_new[:, count] = np.array([float(x1), float(x2)])
            S_new[:, count] = mgc.test(X_new[:, count])
            S_res[int(x2 - test_range[0]), int(x1 - test_range[0]), :] = S_new[:, count]
            count += 1

    plt.imshow(S_res)


def main():
    N1 = 50
    N2 = 60
    N3 = 70
    X = np.zeros((2, N1+N2+N3))
    S = np.zeros((3, N1+N2+N3), 'int8')

    #クラス1の学習データ
    mu1 = np.array([45, 25])
    A = np.array([[3,0],[0,8]])
    sigma1 = np.dot(A.T, A)
    X[:, :N1] = np.random.multivariate_normal(mu1, sigma1, N1).T
    S[0,:N1] =1

    #クラス2の学習データ
    mu2 = np.array([35, 40])
    A = np.array([[5, 3],[3,7]])
    sigma2 = np.dot(A.T, A)
    X[:, N1:N1 + N2] = np.random.multivariate_normal(mu2, sigma2, N2).T
    S[1,N1:N1 + N2] = 1

    #クラス3の学習データ
    mu3 = np.array([30, 25])
    A = np.array([[7,-5],[-5,7]])
    sigma3 = np.dot(A.T, A)
    X[:, N1 + N2:]= np.random.multivariate_normal(mu3, sigma3, N3).T
    S[2,N1 + N2:] = 1

    #事前分布の超パラメータ
    alpha0 = np.random.randn(3)
    m0 = (mu1 + mu2 + mu3)/2
    invW0 = np.linalg.inv((sigma1 + sigma2+ sigma3)/3)
    beta0 = 1.0
    nu0 = m0.shape[0]

    #推論オブジェクトの生成
    mgc = mixture_gaussian_classifier(alpha0, m0,invW0, beta0, nu0)

    fig = plt.figure()
    idx = [i for i in range(X.shape[1])]
    random.shuffle(idx)

    global used_idx
    used_idx = []
    #結果のアニメーション表示（300msごとに関数updateを呼び出す）
    ani = anm.FuncAnimation(fig, update, fargs = (idx, mgc, X, S),
                            interval = 300, frames = N1 + N2+ N3)
    ani.save("result.gif", writer="imagemagick")

if __name__ == '__main__':
    main()

そして、こちらが結果です。

f:id:YamagenSakam:20190210212509g:plain

この図で、各色がそれぞれのクラスを表し、追加されていく各点が学習データを表しています。また、背景色が予測分布が算出した各座標点の各クラスへの所属確率を表しています。
特に左上に辺りの領域に着目すると、最初の方は青色のクラスと予測されていましたが、青と緑のクラスのデータを観測していくにつれ、緑色のクラスだと予測されるようになっていくのがわかります。これは青色のクラスが左下から右上にかけての共分散が大きいのに対し、緑色のクラスの共分散が左上から右下への共分散が大きく、その特徴をサンプルが増えるにつれ、正しく推論できるようになっていくためだと考えられます。

まとめ

今回、ガウス混合分布を用いた教師あり分類をベイズ推論の枠組みを適用して実装してみました。教師ありの分類の場合は、ガウス混合分布モデルによる予測は解析的に求めることができます。
ベイズ推論の枠組みで分類を行う場合は他にもロジスティック回帰をベイズの枠組みで定式化する方法などがあります。今後は、このベイズロジスティック回帰を含めもう少し複雑なモデルを学び実装していきたいと思います。